An international team of scientists has discovered a new form of insulating material with a metallic surface that could enable more-efficient electronics, or even quantum computing. Their findings were facilitated by the development of a new method for analyzing existing chemical compounds that relies on the mathematical properties that govern the repeating patterns seen in everyday wallpaper.
The research, published in the journal Science, involved a collaboration among groups from the University of Pennsylvania, Princeton University, Sungkyunkwan University, Freie Universität Berlin, and the Max Planck Institute of Microstructure Physics.
The discovery of this phase in crystals of lead-strontium, Sr2Pb3, completes a decade-long search for an elusive three-dimensional material that combines the unique electronic properties of two-dimensional graphene and three-dimensional topological insulators, a phase of matter discovered in 2005 in independent works by Penn physicist Charles Kane and Princeton’s B. Andrei Bernevig. Topological insulators are materials that are insulators on their interior but conduct electricity on their surface. Their special properties as efficient conductors have driven speculation that they could serve as a foundation for super-fast quantum computing.
“You can think about a topological insulator like a Hershey’s Kiss,” says Kane, a corresponding author on the paper and the Christopher H. Browne Distinguished Professor of Physics at Penn. “The chocolate is the insulator, and the foil is a conductor. We’ve been trying to identify new classes of materials in which crystal symmetries protect the conducting surface. What we’ve done here is to identify the simplest kind of topological crystalline insulator.”
The new work demonstrates how the symmetries of certain two-dimensional surfaces, known as the 17 wallpaper groups for their wallpaper-like patterning, constrain the spatial arrangement, or topology, of three-dimensional insulators. The researchers applied these constraints to discover phenomenologically distinct topological insulating phases in real materials and also to construct a framework for understanding and diagnosing symmetry-enhanced topological phases, in which the presence of symmetries allows for the existence of the special features in the material’s electronic structure. They also introduce a new set of principles that govern the surface states of topological insulators.
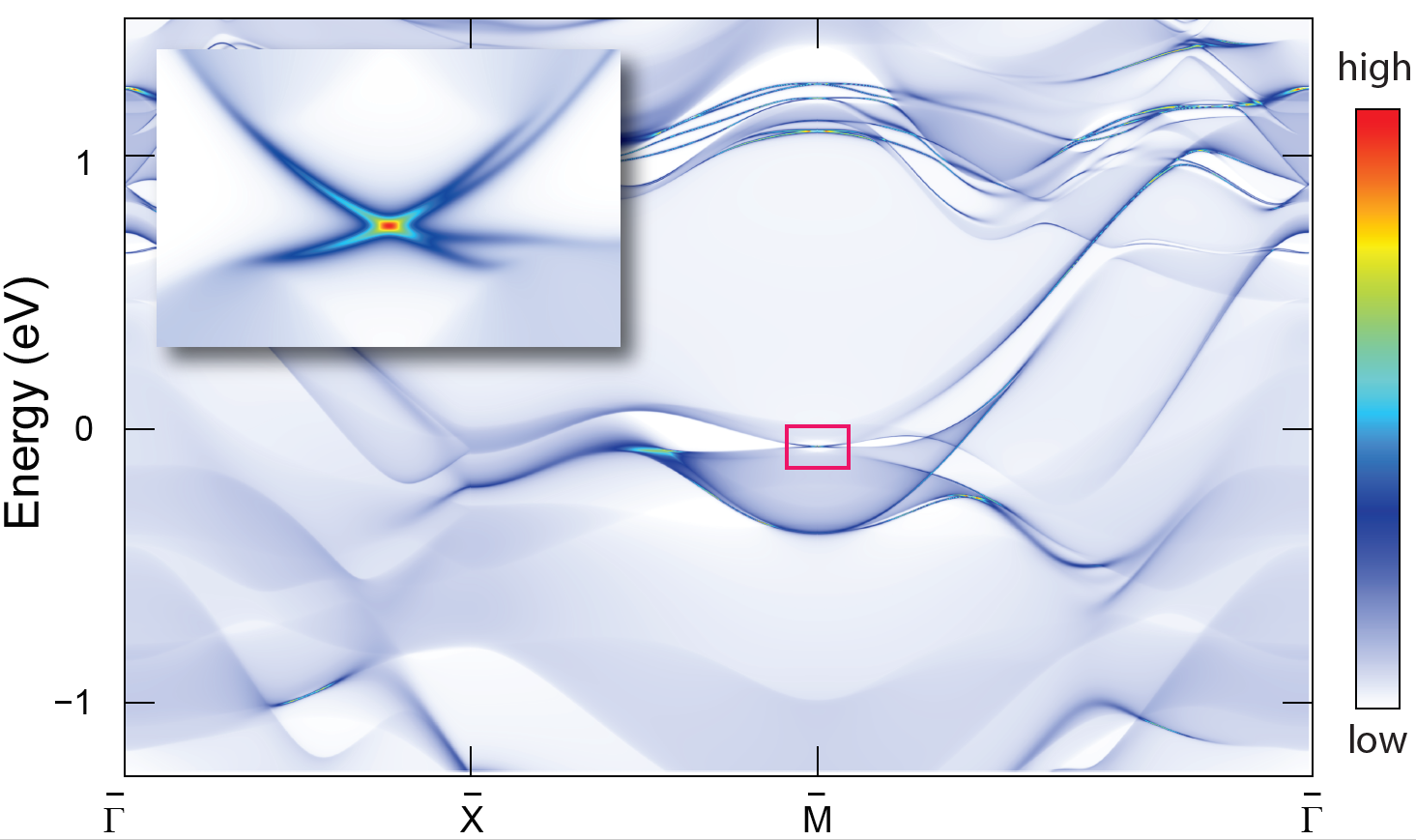
In a conventional three-dimensional topological insulator, each two-dimensional surface exhibits a single characteristic group of states with cone-like dispersion. These cones resemble the elements on graphene called Dirac cones, features that imbue the material and other two-dimensional Dirac semimetals with their unusual electronic-transport qualities. Yet these elements on the new material are distinct because graphene possesses a total of four Dirac cones in two pairs that are “glued” together.
Kane had suspected that, with crystal symmetries, a second kind of topological insulator could exist with a single pair of glued Dirac cones, like “half” of graphene. “What I realized was that a single pair of Dirac cones is impossible in a purely two-dimensional material, but it might be possible at the surface of a new kind of topological insulator. But when I tried to construct such a state, the two cones always came unglued.”
A solution emerged when Benjamin Wieder, then a graduate student in Kane’s group and now a Princeton postdoctoral associate, visited Princeton. There, Bernevig and colleague Zhi Jun Wang had just discovered “hourglass insulators”—topological insulators with strange patterns of interlocking hourglass-like states—which Wieder recognized as acting as if a three-dimensional crystal had been wrapped with a special kind of patterned wallpaper.
“We realized that you could get not just the hourglass insulator, but also this special Dirac insulator, by finding a crystal that looked like it was covered in the right wallpaper,” says Wieder.
In particular, they recognized that a glued pair of Dirac cones could be stabilized on crystal surfaces with two intersecting lines along which the surfaces look identical after being flipped and turned perpendicularly. These lines, known as glide reflections, characterize the so-called nonsymmorphic wallpaper groups, thus providing the namesake of this new phase, which the team dubs a “nonsymmorphic Dirac insulator.”
The researchers applied mathematical rigor to this recognition, resulting in a new, wallpaper symmetry-based methodology for diagnosing the bulk topology of three-dimensional crystals.
“The basic principles are simple enough that we sketched them on napkins that very evening,” says coauthor Barry Bradlyn of Princeton.
Wang adds, “But they are nevertheless robust enough to predict and understand a [wide variety] of new topological phases in real materials.”
“For the first time, we can directly relate the symmetry of a surface to the presence of desired topological surface states,” says Andrew Rappe, professor of chemistry in Penn’s School of Arts and Sciences. “This allows an elegant and immediately useful means of designing desirable surface and interface states.”
To identify the Dirac insulating phase in nature, the researchers calculated the electronic structures of hundreds of previously synthesized compounds with surfaces with two glide lines (wallpaper groups pgg and p4g) before identifying the novel topology in lead strontium. The computational chemists “knew they were searching for a needle in a haystack, but nobody bothered to tell them how small the needle might be,” says Jennifer Cano of Princeton.
As even more exotic topological insulators are discovered, the role of wallpaper group symmetry and of the special, graphene-like cones in the Dirac insulator have been further solidified.
“When you can split a true surface Dirac cone while keeping time-reversal symmetry, something truly special happens,” says Bernevig. “You get three-dimensional insulators whose two-dimensional surfaces are also a kind of topological insulator.” Such phases have been predicted recently in bismuth crystals and molybdenum ditelluride (MoTe2) by several members of the collaboration. Furthermore, with the use of a new theory, topological quantum chemistry, the researchers hope to find many more of these exotic phases.
“If we could paint these materials with the right wallpaper, we’d see more Dirac insulators,” notes Wieder, “but sometimes, the wrong wallpaper is interesting, too.” Adds Bernevig, “The beauty of topology is that one can apply symmetry principles to find and categorize materials.”
The report was coauthored by Princeton’s Wieder, Cano, Barry Bradlyn, Zhi Jun Wang, and B. Andrei Bernevig; Sungkyunkwan’s Youngkuk Kim and by Hyeong Daniel Kim, Rappe, and Kane at the University of Pennsylvania.
The work was supported in part by the Simons Foundation (grants ERC DM 321031 and ONR-N00014-14-1), Nordita, the U.S. Department of Energy (Grant DE-SC0016239), the National Science Foundation (grants DMR-1643312, DMR-1120901, and DMR-1420541), the Packard Foundation, the Schmidt Fund for Innovative Research, and the National Natural Science Foundation of China.









